Describing difficult spaces

The idea behind this curatorial project is to give artists a prompt describing a space that is difficult to visualise, and ask them to come up with a way of describing that space whether that be a visual, auditory, or literary description.

What would it be like to be inside a 3-torus? A space where everything in front of you is behind you, everything to the left of you is to the right and everything above you is below.

Most of the spaces that we work with as mathematicians are hard to imagine devoid of their mathematical description. This is because they often require higher dimensions to visualise than we have the capacity to imagine. As an example the 2-torus (the surface of a donut) is a 2-dimensional surface which can be visualised by embedding it in 3-dimensions. This view shows the space from the outside. If you were on this space, you wouldn’t see this view.

However we can visualise it in 2-dimensions as a quotient space by identifying opposite edges of a square. This is called a gluing diagram:

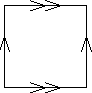
[Image: UIUC]

You can imagine forming the donut shape by folding the square so that the left side is “glued” to the right and the top is “glued” to the bottom.

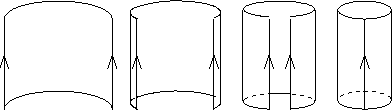
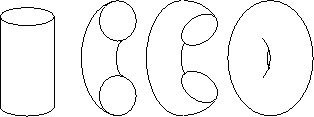
[Image: UIUC]

Another way of visualising these spaces is with a repeating view known as a tiling picture. This represents what the space would look like to someone on it.

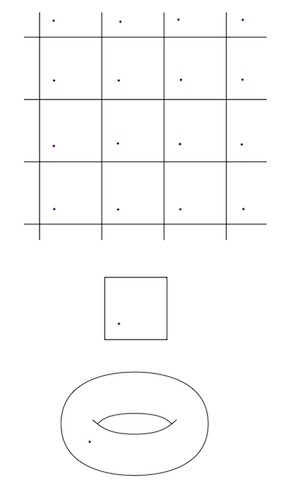
[Image: Scientific American]

Similarly we can visualise a 3-torus by identifying opposite faces of a cube. There is also a tiling picture for this space. However, we don’t have an extra dimension that we can “fold” it into in order to see what this space would look like from outside of it.

[Image: UIUC]

I think what’s interesting about an auditory description of these spaces is that sound has a physical correlate: the waves that produce it. These waves will travel differently depending on the space they’re in.

How does being in a 3-torus affect the way we perceive sound?

If the project goes well, I would like to develop a web platform devoted to it. On this platform will be a number of prompts describing mathematical spaces and anyone will be able to submit a description of these spaces. The idea is to crowdsource these descriptions, and maybe they will converge.

• The Geometry Centre has a project in relation to the book The Shape of Space by Jeffrey R. Weeks. There is an accompanying video which you might find helpful.

• They also have an article which is directly related to the content of this blog post.

• Scientific American has an article on the 2-torus and 3-torus.

Tags: differential geometry art