Is the double twisted Möbius strip isotopic to the ordinary strip in real 3-space?
February 28, 2021
Over the past couple days I have been watching Tadashi Tokieda’s Topology and Geometry lectures, given at AIMS.
I thought they would help me prepare for my first point-set topology course. The material is very different, but I think the lectures will help my intuition. Regardless, they have been a lot of fun.
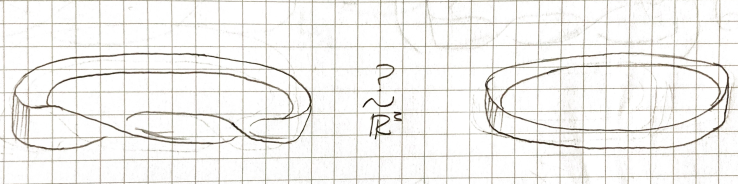
In one of the lectures Tokieda gives a project: is the double twisted Möbius strip isotopic to the ordinary strip in $\mathbb{R}^3$?
Before we can think about answering this question, there is some background knowledge from the lectures that you need to know.
The definitions, theorems, and examples in this post come from Professor Tokieda’s lectures (mainly, lecture 5 part 1, part 2 and lecture 6 part 1, part 2). Most of the diagrams are my own attempt at his. Obviously, any errors are my own.
What is overflow?
In $\mathbb{R}^2$, two lines ($dim1$, $dim1$) generically intersect in a point ($dim0$). Of course, there are cases of lines that do not intersect but these lines are degenerate. $$1+1-2=0$$
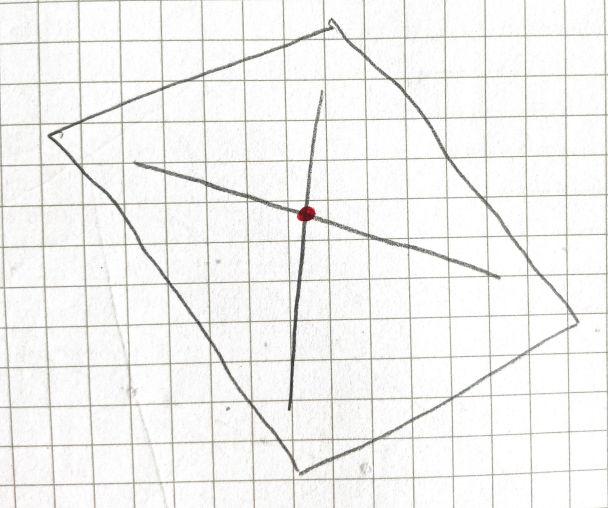
In $\mathbb{R}^3$, a line ($dim1$) and a plane ($dim2$) generically intersect in a point ($dim0$). $$1+2-3=0$$
Two planes ($dim2$, $dim2$) generically intersect in a line ($dim1$). $$2+2-3=1$$
These examples follow a pattern, revealing how much dimension overflows when we try to fit two submanifolds into a larger ambient manifold. The following theorem formalizes this pattern.
Theorem
Let $K,L$ be submanifolds of $M$ and let $dimK+dimL-dimM$ denote the overflow.
If $\text{overflow}<0$ then generically $K\cap L=\emptyset$.
If $\text{overflow}\geq0$ then generically $K\cap L \neq \emptyset$ and $dim(K\cap L)=\text{overflow}$.
Hence, after trying to fit $K$ and $L$ into $M$, negative overflow means there is still space available in the ambient manifold $M$ such that, generically, $K$ and $L$ don’t intersect. If the overflow is positive, then it gives the dimension of the intersection of $K$ and $L$.
What is isotopy?
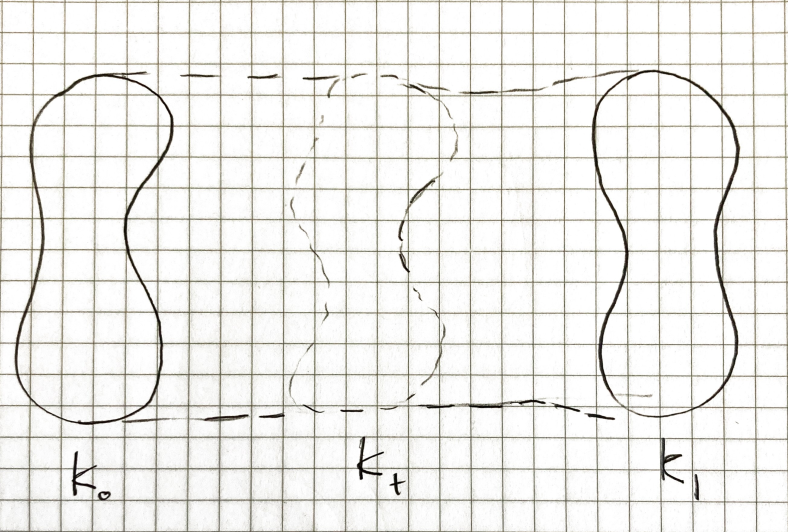
Definition
Imagine we are moving a submanifold $K$ in an ambient manifold $M$, and denote the position of $K$ at time $t\in [0,1]$ by $K_t$. If $K_t$ never has self-intersections at any $t$, then we say $K_0$ is isotopic to $K_1$ in $M$, written, $K_0\sim_M K_1$.
This relation is weaker than homeomorphism since an isotopy implies a homeomorphism, but the converse is not true. That is, a homeomorphism is a necessary condition for an isotopy but it is not sufficient.
$$K_0\sim_M K_1\implies K_0\approx K_1$$
You will need the contrapositive (if there is no homeomorphism, then there is no isotopy) for an exercise at the end, so remember it.
If you don’t know what a homeomorphism is, it’s basically any continuous deformation of one manifold into another. The continuous part is a requirement that the deformation doesn’t tear (or break holes in) the manifold. As an example that everyone gives, a coffee mug is homeomorphic to a torus (surface of a donut) but the surface of a sphere is not.
Before we take a look at some examples of isotopy, you need to know how it relates to overflow.
How does overflow relate to isotopy?
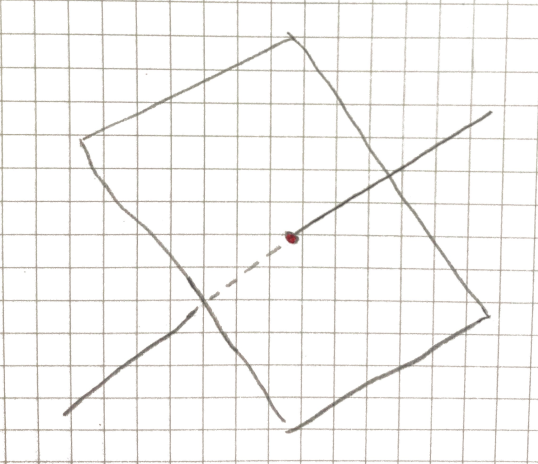
In $\mathbb{R}^2$ a point ($dim0$) moving from one side of a line ($dim1$) to the other must intersect the line.
However, in $\mathbb{R}^3$, the point can avoid intersecting the line.
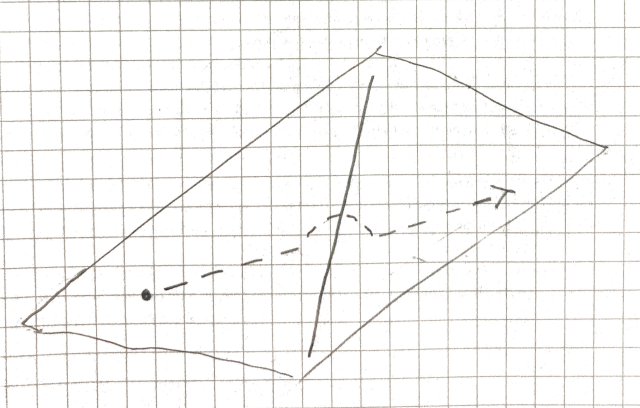
In $\mathbb{R}^3$, a line moving from one side to the other of a line, must intersect.
But in $\mathbb{R}^4$, the line can avoid the crossing.
Theorem
Let $K,L$ be submanifolds of $M$ such that $\text{overflow}=dimK+dimL-dimM<0$ so that initially $K\cap L=\emptyset$. Suppose $K$ moves from the one side to the other side of $L$, and tries to avoid crossing $L$.
If $\text{overflow}=-1$ then crossing is inevitable.
If $\text{overflow}<-1$ then crossing is avoided.
Why $-1$? Well, moving $K$ sweeps out a sheet of $dimK+1$. In order for $K$ not to have intersected $L$ at any point in the movement, there must be enough space in the ambient manifold for the sheet to avoid $L$.
$$\text{sheet}\cap L=\emptyset \iff 1+dimK+dimL-dimM < 0$$
Hence, $dimK+dimL-dimM < -1$.
We can use this theorem to learn a really interesting property of knots.
Corollary
Every knot (made of curves) can be unknotted in $\mathbb{R}^m$ for all $m\geq4$.
If we want to turn a knot of curves into the unknot we need to be able to make the below moves in whatever ambient manifold we’re in.
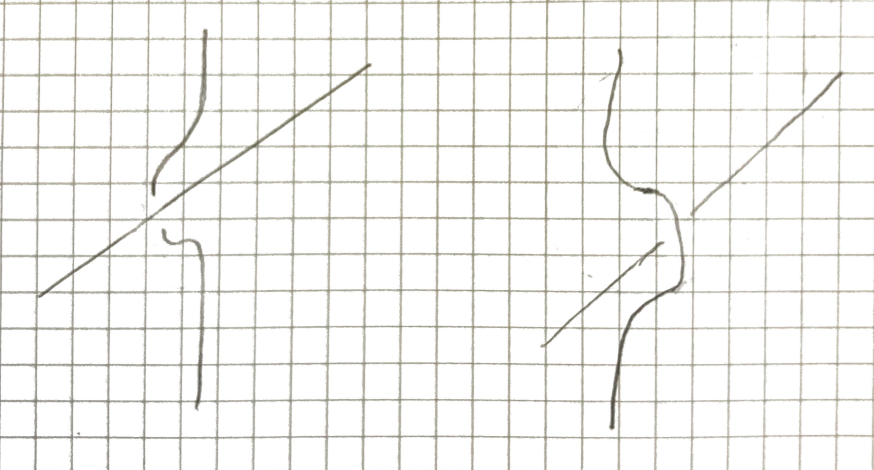
There must be enough space in the manifold to move two lines of dimension 1 across each other without them intersecting. This gives the following inequality.
$$\text{overflow} = 1 + 1 - m < -1 \implies m \geq 4$$
Hence, in $\mathbb{R}^4$ and above, all knots of curves are the unknot.
What this example shows is that the question of whether a knot can be unknotted in a particular ambient manifold is the same as asking whether that knot is isotopic to the unknot in that manifold.
An easy exercise: in what dimension can the trefoil knot of a 2 dimensional surface be unknotted?
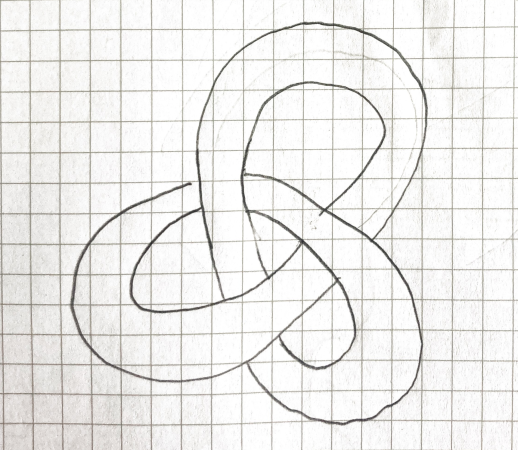
We can use overflow to define a sufficient condition for isotopy, namely, two submanifolds are isotopic in an ambient manifold if their overflow in that manifold is less than $-1$.
But this is not a necessary condition as we will see in the following example.
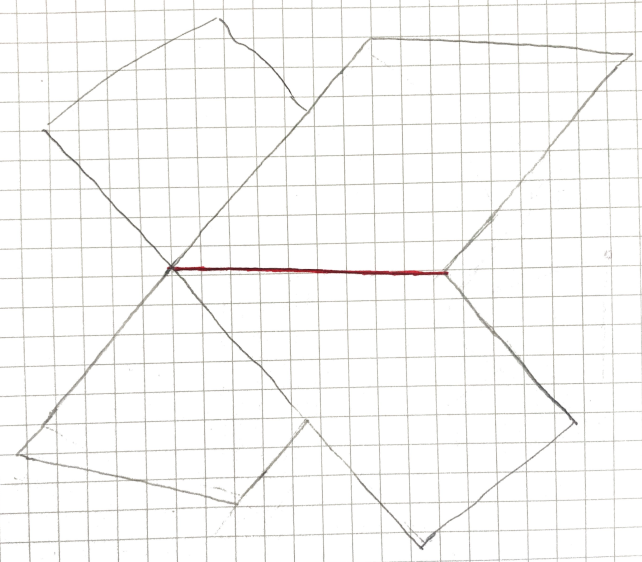
Are the following manifolds isotopic in $\mathbb{R}^3$?
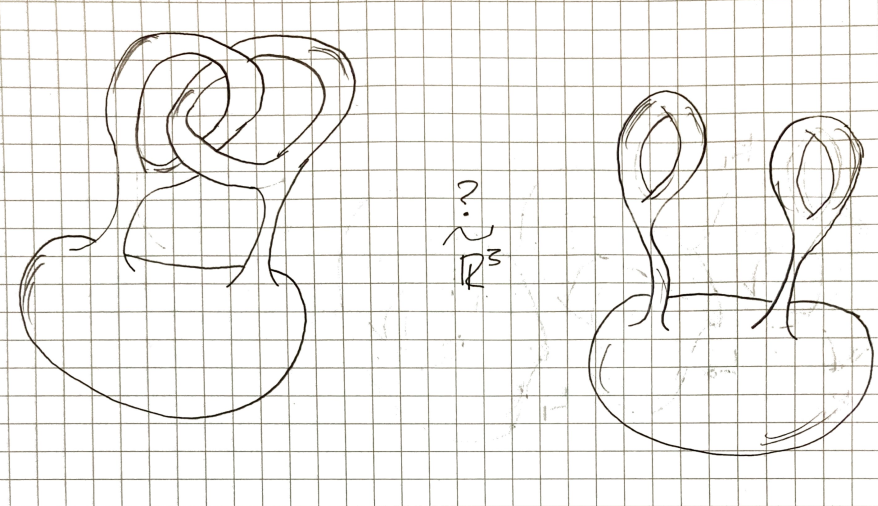
Obviously, by the previous theorem they are isotopic in $\mathbb{R}^6$ and above, but, is there enough space in $\mathbb{R}^3$ to undo the linked loops without intersecting the manifold?
Turns out there is.
We start by widening the loops.
Continuing to widen them until we get two legs connecting to the surface.We can then take the two legs that are twisted around each other and, sliding them across the surface of the sphere, untwist them.
Leaving us with the surface we wanted to isotope to.
Here’s a second example. Consider the Riemann surface of genus 3, denoted $\Sigma_3$ (if you don’t know what that is, it’s a 2-dimensional surface with 3 holes in it) and four loops around the surface.
Can we isotope $K_0$ to $K_1$ and $L_0$ to $L_1$ in $\Sigma_3$?
It should be easy to see that $K_0\sim_{\Sigma_3}K_1$ since we can slide $K_0$ around the hole into $K_1$.
It is less straightforward with $L_0$ and $L_1$.
In fact, $L_0\not\sim_{\Sigma_3}L_1$, since, in moving $L_0$ to the position of $L_1$, we inevitably have to move over one of the holes.
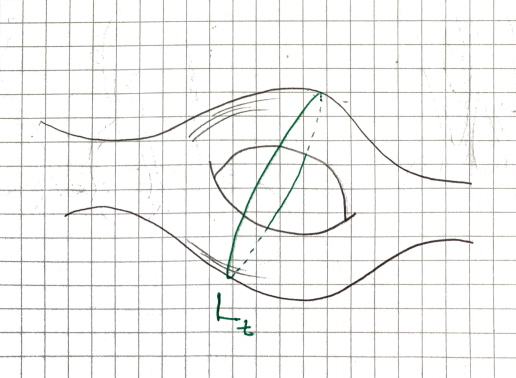
The space in the hole is not a part of the surface $\Sigma_3$ and hence, we cannot isotope $L_0$ to $L_1$ in $\Sigma_3$.
This is where you try to solve the problem.
Is the double twisted Möbius strip isotopic to the ordinary strip in $\mathbb{R}^3$?
The Möbius strip with two twists and the ordinary strip are homeomorphic to one another since they are both orientable surfaces, that is, they are both homeomorphic to the Riemann surface of genus 1 (surface of a donut).
They are also isotopic in $\mathbb{R}^m$ for $m\geq 6$ since, in $\mathbb{R}^6$ and above, there is enough ambient space to untwist the Möbius strip without intersecting it. However, in $\mathbb{R}^3$, trying to remove a twist in the Möbius strip, without intersecting it, moves the twist along the strip.
My intuition here was that they are not isotopic in $\mathbb{R}^3$ since, in order to remove a twist from the Möbius strip it is necessary to make a self-intersecting move or a cut and a glue.
But how do we show this?
The issue we would need to resolve in order to make the deformation is how to untangle two curves that go around the Möbius strip, one on the inside and one on the outside.
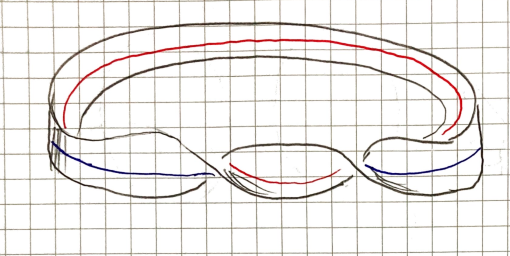
In order to obtain these curves we can take the boundary of the double twisted Möbius strip.
Let us denote the ordinary strip by $\mu(0)$ and the double twisted Möbius strip by $\mu(2)$ (the reason for this will become apparent in the next part, for now, it’s a lot easier to write).
The boundary of $\mu(0)$, $\partial\left(\mu(0)\right)$, is the union of two circles.
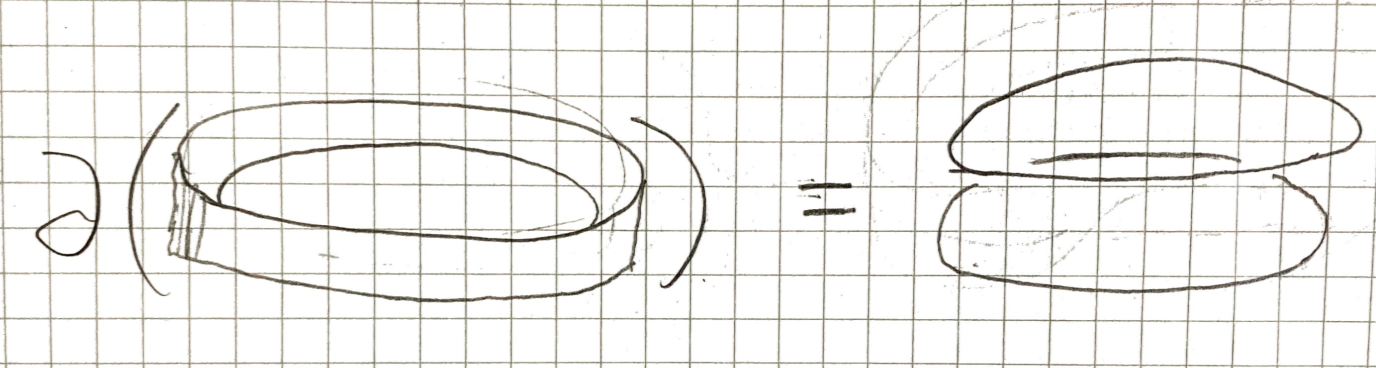
The boundary of $\mu(2)$, $\partial\left(\mu(2)\right)$, is a knot of two curves.
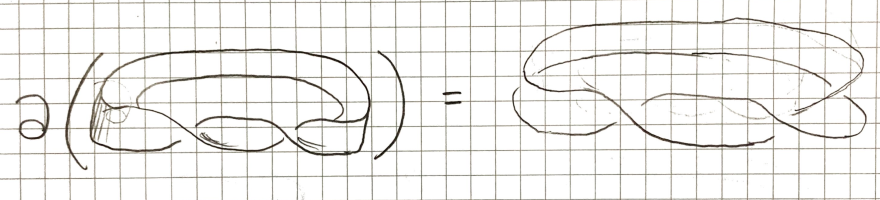
If we move the boundary of $\mu(2)$ around a bit we can see it is in fact the Hopf link.
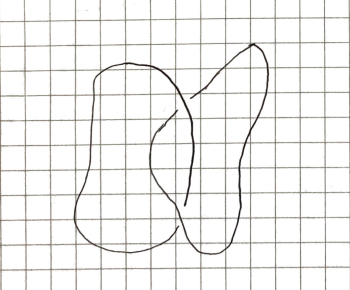
It should now be obvious to you that there is no way to isotope $\mu(2)$ to $\mu(0)$ in $\mathbb{R}^3$ since there is no way to isotope $\partial\left(\mu(2)\right)$ to $\partial\left(\mu(0)\right)$ in $\mathbb{R}^3$.
Any deformation of $\mu(2)$ into $\mu(0)$ requires a self-intersecting move in order to unlink the boundary of the Möbius strip since the question reduces to whether we can unknot the Hopf link in $\mathbb{R}^3$.
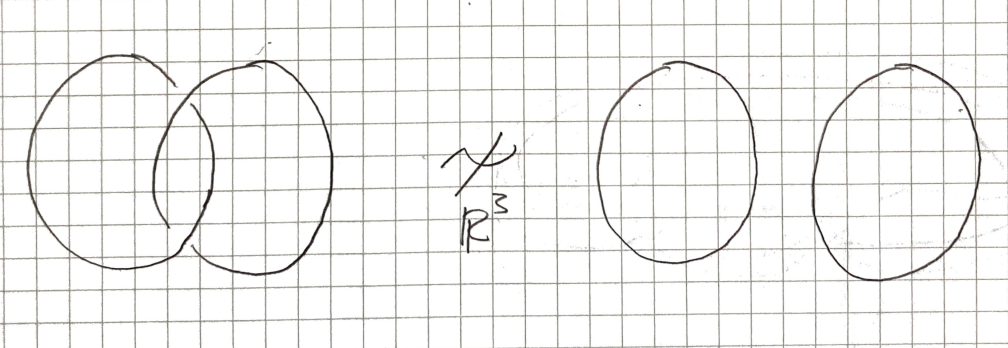
Which we can’t do.
More generally, if $M$ is a manifold and $K,L$ submanifolds of $M$ then $$\partial(K)\not\sim_M\partial(L)\implies K\not\sim_M L$$ since $\partial(K)\subseteq K$ and the condition for isotopy is that $K$ not intersect itself.
Now it’s time to generalize.
Is the n-twisted Möbius strip isotopic to the (n+1)-twisted or (n+2)-twisted Möbius strip in $\mathbb{R}^3$?
Let us denote the n-twisted Möbius strip by $\mu(n)$. Now we can ask three interesting questions:
Can we isotope $\mu(n)$ to $\mu(0)$?
Can we isotope $\mu(n+1)$ to $\mu(n)$?
Can we isotope $\mu(n+2)$ to $\mu(n)$?
I’ll leave these to the reader to figure out, they should be easy.
Retrospective September 2024
After releasing this blog post, accompanying the creation of my website, I contacted Scott Aaronson (shtetl-optimized). He was kind enough to give me very encouraging feedback. Consider the audience. The intended audience for this website changed after this.
Dear Prof Aaronson,
I was hoping I could get your advice on whether I should start a math blog, I know you started yours while you were quite young.
I am a third year undergrad math and cs major at Wits in Johannesburg, South Africa and an avid reader of your blog and book. (I’m pretty sure this was a glitch in the local website, but there were copies of your book for the equivalent of $4.50, I quickly sent it to all my friends and lecturers).
I recently created a portfolio website and I would like to include a blog to record and present my thinking. I think it will help me focus my learning and allow me to work with the material for longer before moving on.
Ideally I would be breaking down my thought process in trying to solve a question like “is the double twisted Möbius strip isotopic to the regular strip?”
On the one hand, I would like my writing to be representative of my thinking, but on the other, I am afraid that any mistakes I make will leave a bad impression. I am still learning, so this is bound to happen. Will these mistakes matter for my academic career? Or will people understand that I’m an undergrad and it’s a blog? Do you think it’s worth the risk? . . .
Dear Elias,
Nice to e-meet you!
I don’t see any downsides to the math blog that you’re describing, other than the time investment on your part! If it’s something you want to do, go for it.
I’ve been blogging for over 15 years now. I’ve gotten pushback for many different types of posts — about D-Wave, criticizing wrong papers, etc, and obviously also about politics and social justice issues. There is, of course, a clear (though far from perfect) correlation between posts that attract a large readership, and posts that stick their neck out and say something that somebody will object to! But it’s hard to imagine getting much pushback for a post about the double-twisted Möbius strip.
Good luck!! And send me a link once it’s up.
Best, Scott
. . . I set up my website and wrote the first blog post. Let me know what you think if you get the chance to read it. I’d love to hear any comments or if you find any errors. I’m particularly interested in the latter. . .
. . . Sorry for the delay! I just read your post. This is really beautiful material. But my central piece of advice is this: by heavily using mathematical notation and definitions, you cut your potential readership by a factor of maybe 1000. Now, if the notation and definitions were actually essential to understanding the meat, that would be fine. But this is the kind of topology that people can just visualize in their heads, with the aid of the sort of pictures that you already have! As an exercise, I might try completely rewriting your post the way Martin Gardner would have written it – in a way where it was completely accessible to 8-year-olds and grandmas. (“Did you know that you can unlink these two rings without cutting anything? Did you know that you can untie any knot if you go up to the 4th dimension? Let me show you how!”) That would mean no equations whatsoever, and no terms like “isotopic” until AFTER you’ve carefully explained them in plain English (and even then, only sparingly).
The key is to treat it as an intellectual challenge to see just how much of the intellectual content you can get across while adhering to those rules.
Or if you don’t want to, that’s fine too! But I’m the one you asked for advice. :-D . . .